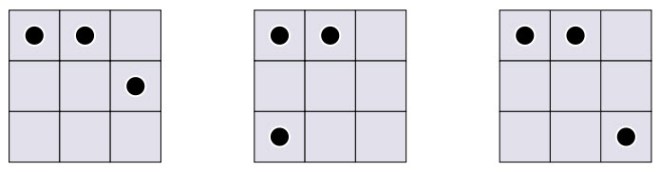
Es fácil colocar 3 fichas en las casillas de un damero 3 x 3 de modo que no haya nunca 2 pares de fichas a la misma distancia. Se supone que cada ficha señala el centro exacto de una casilla y que las distancias se miden sobre una línea recta que une los centros. Salvo giros y simetrías, existen tres soluciones, como se muestra en la imagen.
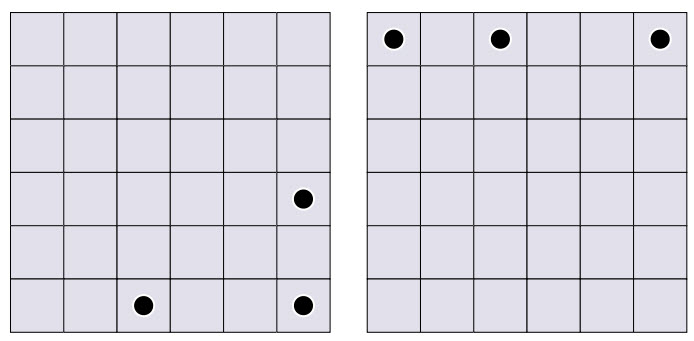
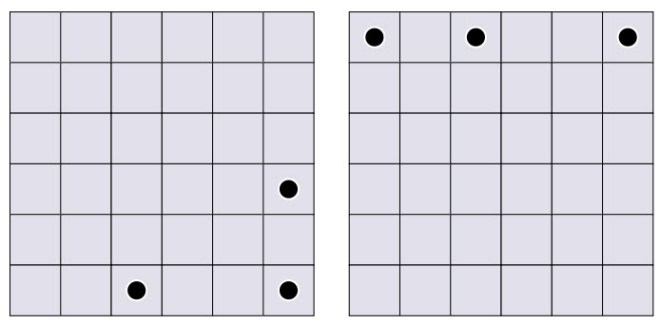
La solución para un cuadrado de orden 6 resulta difícil porque por primera vez entra en escena el triángulo rectángulo de lados 3, 4 y 5 (la terna pitagórica mínima). El número de disposiciones queda muy reducido debido a que son posibles distancias de 5 unidades tanto en filas y columnas como en diagonal. Sólo hay dos soluciones, ¿puedes encontrar alguna?. Como pistas daré la colocación de tres fichas en cada una de las soluciones.
Para un cuadrado de orden 7 sólo existe una solución dificilísima de encontrar a menos que se programe por ordenador. Ahora bien, por probar a mano, quién sabe si darás con ella?. Está demostrado que el cuadrado de orden 7 es el menor cuadrado con solución para cuadrados de orden n con n fichas.
Distancias diferentes
Es fácil colocar 3 fichas en las casillas de un damero 3 x 3 de modo que no haya nunca 2 pares de fichas a la misma distancia. Se supone que cada ficha señal
meganicho
es
https://oyequotes.com/static/images/meganicho-distancias-diferentes-10216-0.jpg
2024-12-12



Si crees que alguno de los contenidos (texto, imagenes o multimedia) en esta página infringe tus derechos relativos a propiedad intelectual, marcas registradas o cualquier otro de tus derechos, por favor ponte en contacto con nosotros en el mail bitelchux@yahoo.es y retiraremos este contenido inmediatamente