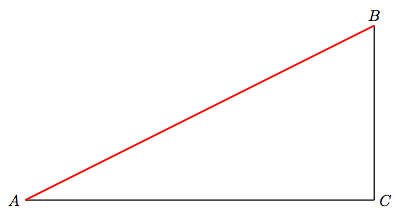
Supongamos el siguiente Teorema:
En un triángulo rectángulo , la suma de las longitudes de los catetos es igual a la hipotenusa.
(Las definiciones de los conceptos son los habituales)
Pues entonces , pasemos a demostrar ese ¿absurdo? teorema.
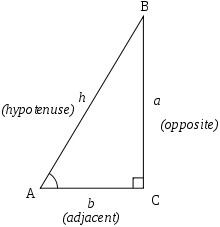
Partimos del triangulo
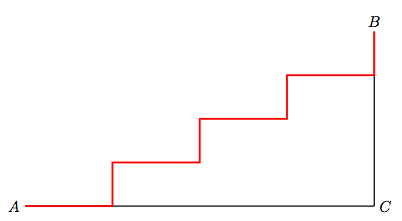
Y construimos la «hipotenusa» a base de escalones de tal manera
Te recomendamos Vinos de Granada
Se aprecia claramente ( no hay más que «trasladarlos» vertical y horizontalmente sobre los ejes) que la suma de los segmentos desde A hasta B , son igual a la suma de los 2 catetos AC + CB.
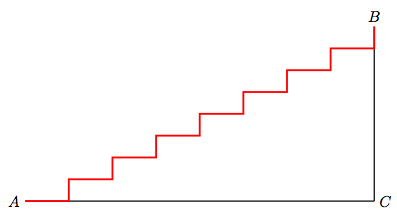
Seguimos con mas «escalones»
y sigue claramente manteniendose la igualdad , por lo que si lo llevamos al limite de escalones , tendremos una hipotenusa recta que es la suma de los infinitos escalones y es igual a la suma de los catetos.
¿Dónde está el error en la demostración?
Visto en el blog de Francisco Blanco-Silva
Falacia geométrica.
En un triángulo rectángulo , la suma de las longitudes de los catetos es igual a la hipotenusa. Supongamos el siguiente Teorema: Supongamos el siguiente Teor
meganicho
es
2025-05-06
Si crees que alguno de los contenidos (texto, imagenes o multimedia) en esta página infringe tus derechos relativos a propiedad intelectual, marcas registradas o cualquier otro de tus derechos, por favor ponte en contacto con nosotros en el mail bitelchux@yahoo.es y retiraremos este contenido inmediatamente